Difference between revisions of "How to interpret WRF variables"
(→Grid) |
(→Wind) |
||
| Line 19: | Line 19: | ||
==Wind== | ==Wind== | ||
| − | Components of the wind velocity vector '''U''', '''V''', '''W''' live at the corresponding points, hence the point names. These are in the geometrically horizontal and vertical directions. On flat ground, '''W''' on the first level ''k=1'' is zero. However, when the ground has nonzero slope, the vertical velocity components '''W''' is generally not zero, because the normal vector to the ground is not vertical. | + | Components of the wind velocity vector '''U''', '''V''', '''W''' live at the corresponding points, hence the point names. These are in the geometrically horizontal and vertical directions. On flat ground, '''W''' on the first level ''k=1'' is zero. However, when the ground has nonzero slope, the vertical velocity components '''W''' is generally not zero, because the normal vector to the ground is not vertical. |
| + | |||
| + | Because the components of the wind velocity vector are on different staggered grids, and visualization software usually expects all three components of the velocity vector based at the same point, they need to be interpolated to cell centers for display: | ||
| + | : '''U_DISPLAY(i,j,k) = 0.5*(U(i,j,k) + U(i+1,j,k))''' | ||
| + | : '''V_DISPLAY(i,j,k) = 0.5*(V(i,j,k) + V(i,j+1,k))''' | ||
| + | : '''W_DISPLAY(i,j,k) = 0.5*(W(i,j,k) + W(i,j,k+1))''' | ||
==Location== | ==Location== | ||
Revision as of 01:55, 8 August 2010
Grid
Grids in WRF are logically rectilinear. Variables for WRF cell indexed (i,j,k) can be located at one of 4 possible points. You can tell where by looking at the WRF registry or the attributes of NetCDF files, which WRF uses as I/O format. You can also tell by the fact that staggered variables have the staggered dimension larger by one, since there needs to be variable at the last boundary face.
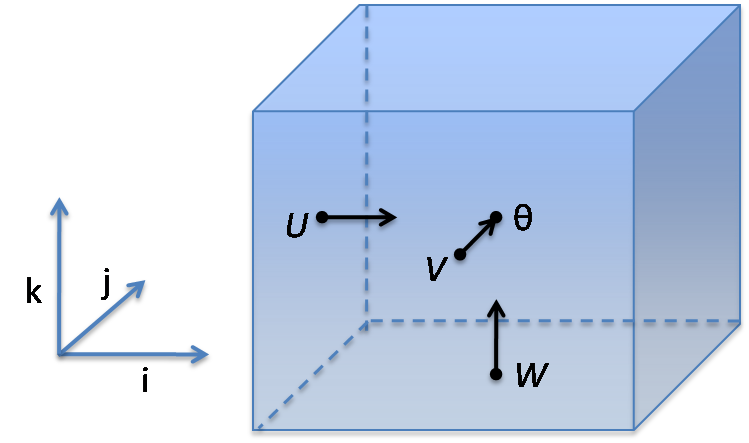
- at the center of the cell - theta points, not staggered
- at the center of the left face - U point, staggered in X
- at the center of the front face - V point, staggered in Y
- at the center of the bottom face - W point, staggered in Z
Scalar variables (such as thermodynamical variables, hence the theta: temperature, pressure,...) generally live at theta-points. One exception is the geopotential, which lives at W-points. The documentation and comments of the code talk about theta-height (mid-level of the cell) and W-height (bottom of the cell).
The orientation of the axes in the real world, such as "east-west", in the order of increasing index, such as i, can be found from the registry, or, preferably, at runtime as attributes in the NetCDF files.
Files
Files are (by default) in NetCDF format. The values associated with the cell (i,j,k) at time step n are stored as the array entry U(i,j,k,n), e.t.c. The value of the time at the step n is stored in character array Times(:,n).
Wind
Components of the wind velocity vector U, V, W live at the corresponding points, hence the point names. These are in the geometrically horizontal and vertical directions. On flat ground, W on the first level k=1 is zero. However, when the ground has nonzero slope, the vertical velocity components W is generally not zero, because the normal vector to the ground is not vertical.
Because the components of the wind velocity vector are on different staggered grids, and visualization software usually expects all three components of the velocity vector based at the same point, they need to be interpolated to cell centers for display:
- U_DISPLAY(i,j,k) = 0.5*(U(i,j,k) + U(i+1,j,k))
- V_DISPLAY(i,j,k) = 0.5*(V(i,j,k) + V(i,j+1,k))
- W_DISPLAY(i,j,k) = 0.5*(W(i,j,k) + W(i,j,k+1))
Location
The longitude and latitude of the theta and U nodes are given by arrays XLONG and XLAT, which are set at initialization and then do not change. However the elevation has to be computed from the flow solution as geopotential height by
- ELEVATION_W = (PHB + PH)/9.81"'
where PHB + PH is the geopotential. PHB is constant, set at initialization, and PH, called perturbation geopotential, varies with time.
PH and PHB live at the W-points, thus the geopotential height at the lowest level is the same as terrain height
- HGT(i,j) = PHB(i,j,1)/9.81
(with the variable names and index order used in the NetCDF files, which is somewhat different from that in the WRF code itself; the mapping is established by the Registry)
To find the elevation of the cell midpoints, you need to interpolate the elevation of the top and the bottom:
- ELEVATION(i,j,k) =0.5*(PHB(i,j,k) + PH(i,j,k) + PHB(i,j,k+1) + PH(i,j,k+1))/9.81
Temperature
Fire variables
See also
- WRF output fields from the WRF-ARW user's guide
- Grid: A Description of the Advanced Research WRF Version 3 (June 2008) Fig 7.3 page 59
- WRF Coding Conventions
- WRF Registry and Examples
- WRF v2 Software Tools and Documentation
- Description of WRF Registry
This page is a stub. You can help by expanding it!