Difference between revisions of "Fuel moisture model"
(Created page with '{{users guide}} Coming soon.') |
|||
| Line 1: | Line 1: | ||
{{users guide}} | {{users guide}} | ||
| − | + | ||
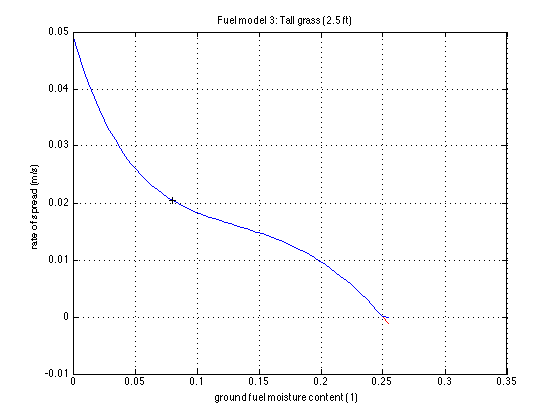
| + | Fire spread rate depends strongly on the moisture contents of the fuel. In fact, the spread rate drops to zero when the moisture reaches the so-called extinction value [[Image:Grass-fmc.png|right|200px]] For this reason, we have coupled the fire spread model with a simple fuel moisture model integrated in SFIRE and run independently at every point of the mesh. The temperature and the relative humidity of the air (from the WRF atmosphere model) determine the fuel equilibrium moisture contents ''E'' , and the actual moisture contents ''m = m (t)'' is then modeled by the standard time-lag equation | ||
| + | :''dm/dt = (E − m)/T'' | ||
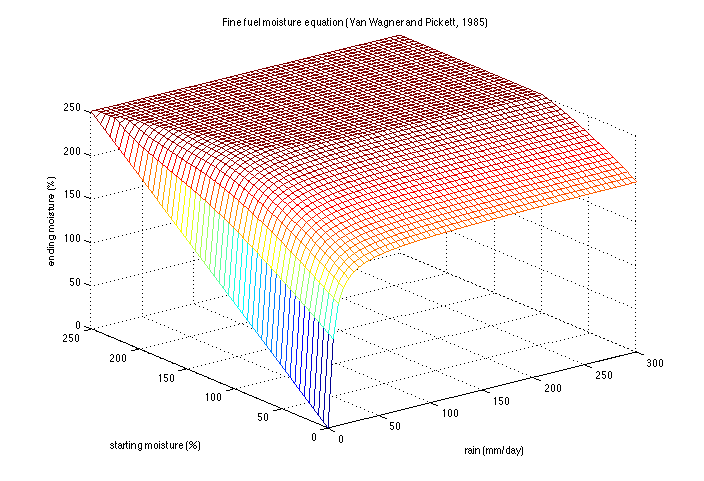
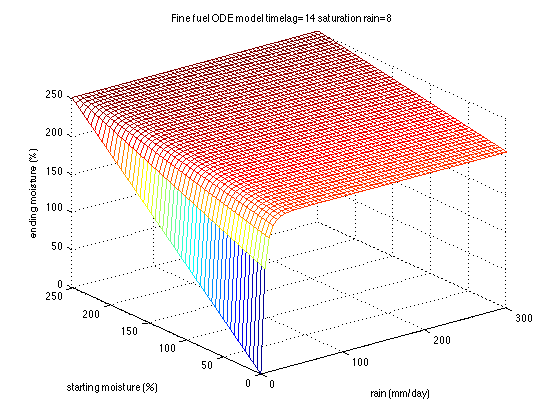
| + | where T is the lag time. We use the standard model with the fuel consisting of components with 1, 10, and 100 hour lag time, with the proportions given by the fuel category. The moisture is computed in each component separately. The equilibrium ''E'' is computed from atmospheric state from WRF. During rain, the equilibrium moisture ''E'' is replaced by the saturation moisture contents, and the equation is modified to achieve the rain-wetting lag time T only asymptotically for heavy rain, | ||
| + | :''dm/dt = (1-exp(-(r-r<sub>0</sub>)/r<sub>s</sub>)(E − m)/T'' | ||
| + | (if ''r > r0''), where ''r'' is the rain intensity, ''r<sub>0</sub>'' is the threshold rain intensity below which no perceptible wetting occurs, and ''r<sub>0</sub>rs'' saturation rain intensity, at which ''1 − 1/e ≈'' 63% of the maximal rain-wetting rate is achieved. | ||
| + | |||
| + | [[Image:finefuels.png|200px]] [[Image:timelag.png|200px]] | ||
| + | ==References== | ||
| + | |||
| + | * Adam K. Kochanski, Jonathan D. Beezley, Jan Mandel, and Minjeong Kim, '''WRF fire simulation coupled with a fuel moisture model and smoke transport by WRF-Chem''', [http://www.mmm.ucar.edu/events/2012_wrfusers/ 2012 WRF Users Workshop], [http://www.openwfm.org/wiki/File:WRF_workshop_2012_poster.pdf Poster 51] [http://www.mmm.ucar.edu/events/2012_wrfusers/abstracts/p51.htm abstract] [https://www.regonline.com/AttendeeDocuments/1077122/43365086/wrf2012.pdf paper] {{arXiv|1208.1059}} | ||
| + | |||
| + | * Jan Mandel, J.D. Beezley, A. K. Kochanski, V. Y. Kondratenko, and M. Kim, '''Assimilation of Perimeter Data and Coupling with Fuel Moisture in a Wildland Fire - Atmosphere DDDAS''', ICCS 2012, [http://dx.doi.org/10.1016/j.procs.2012.04.119 Procedia Computer Science 9, 2012, 1100-1109] | ||
Revision as of 01:08, 24 December 2012
- Back to the WRF-SFIRE user guide.
Fire spread rate depends strongly on the moisture contents of the fuel. In fact, the spread rate drops to zero when the moisture reaches the so-called extinction value
For this reason, we have coupled the fire spread model with a simple fuel moisture model integrated in SFIRE and run independently at every point of the mesh. The temperature and the relative humidity of the air (from the WRF atmosphere model) determine the fuel equilibrium moisture contents E , and the actual moisture contents m = m (t) is then modeled by the standard time-lag equation
- dm/dt = (E − m)/T
where T is the lag time. We use the standard model with the fuel consisting of components with 1, 10, and 100 hour lag time, with the proportions given by the fuel category. The moisture is computed in each component separately. The equilibrium E is computed from atmospheric state from WRF. During rain, the equilibrium moisture E is replaced by the saturation moisture contents, and the equation is modified to achieve the rain-wetting lag time T only asymptotically for heavy rain,
- dm/dt = (1-exp(-(r-r0)/rs)(E − m)/T
(if r > r0), where r is the rain intensity, r0 is the threshold rain intensity below which no perceptible wetting occurs, and r0rs saturation rain intensity, at which 1 − 1/e ≈ 63% of the maximal rain-wetting rate is achieved.
References
- Adam K. Kochanski, Jonathan D. Beezley, Jan Mandel, and Minjeong Kim, WRF fire simulation coupled with a fuel moisture model and smoke transport by WRF-Chem, 2012 WRF Users Workshop, Poster 51 abstract paper arXiv:1208.1059
- Jan Mandel, J.D. Beezley, A. K. Kochanski, V. Y. Kondratenko, and M. Kim, Assimilation of Perimeter Data and Coupling with Fuel Moisture in a Wildland Fire - Atmosphere DDDAS, ICCS 2012, Procedia Computer Science 9, 2012, 1100-1109