Difference between revisions of "Fuel moisture model"
| Line 1: | Line 1: | ||
{{users guide}} | {{users guide}} | ||
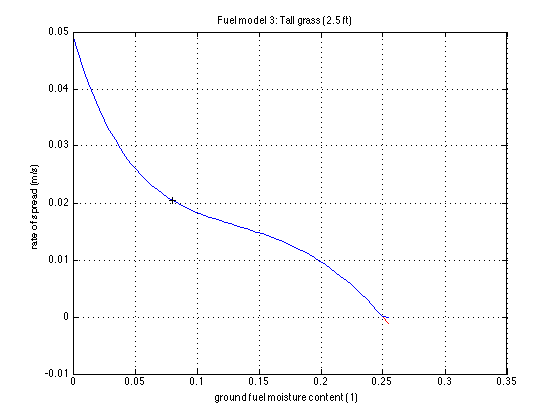
| − | Fire spread rate depends strongly on the moisture contents of the fuel. In fact, the spread rate drops to zero when the moisture reaches the so-called extinction value [[ | + | Fire spread rate depends strongly on the moisture contents of the fuel. In fact, the spread rate drops to zero when the moisture reaches the so-called extinction value [[File:Grass-fmc.png|right|400px|Dependence of fire spread rate (with zero wind and slope) on fuel moisture. The spread rate becomes zero when the fuel moisture equals the extinction moisture, here 0.25.]] For this reason, we have coupled the fire spread model with a simple fuel moisture model integrated with WRF and SFIRE. The model takes atmospheric state from WRF and provides fuel moisture to SFIRE. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Image:finefuels.png| | + | ==Fuel moisture model description== |
| + | The fuel is considered to consist of components - called ''moisture classes'' here - such as those with standard 1, 10, and 100 hour lag time. Each fuel category is a mixture of the moisture classes with the proportions given per the fuel category. The temperature and the relative humidity of the air (from the WRF atmosphere model) determine the fuel equilibrium moisture contents. In each class, the moisture contents approaches the equilibrium exponentially in time, with 63% of the difference gone within the given time lag if the equilibrium is constant in time. This is modeled by a standard time-lag differential equation and the class moisture contents generally tracks a time-varying equilibrium with a delay. To model hysteresis effects, there is a higher drying equilibrium and a lower wetting equilibrium; when the fuel moisture is between the two, it does not change. The equilibria are computed from the atmospheric state from WRF. During rain, the equilibrium moisture is replaced by the saturation moisture contents, and the time lag depends on rain intensity. If the rain intensity is under the given rain threshold, no rain wetting (soaking) takes place. For more intense rain, the time lag decreases and approaches the given soaking time lag exponentially, with 63% of the asymptotic value achieved at a given saturation rain intensity. | ||
| + | |||
| + | ==Calibration of rain wetting== | ||
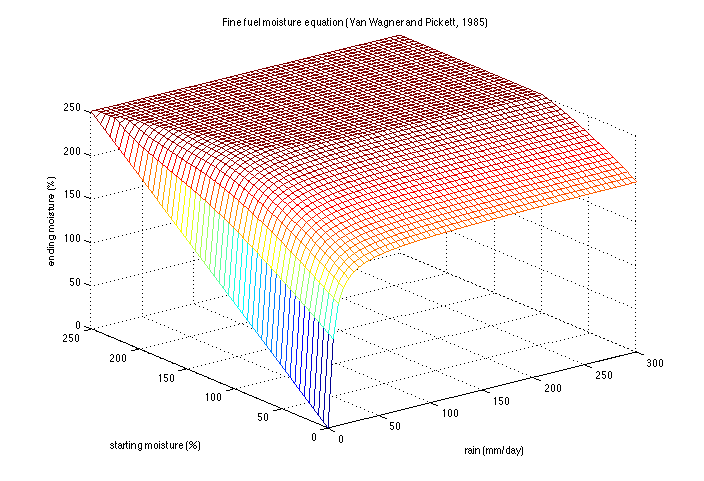
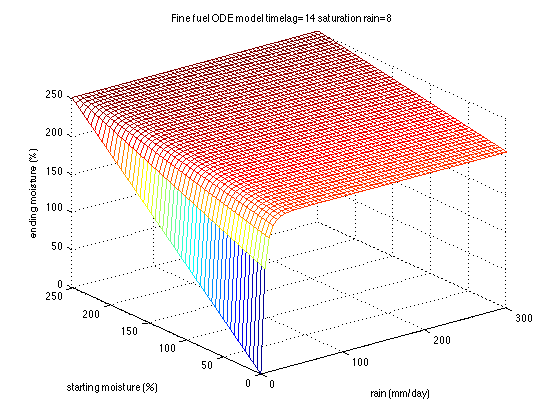
| + | The default rain wetting coefficients were fitted for fine fuels (10 hour moisture class) for the Canadian fire danger rating system. Both pictures show the increase of fuel moisture over 24 hours for a given rain intensity. | ||
| + | |||
| + | [[Image:finefuels.png|400px]] [[Image:timelag.png|400px]] | ||
| + | |||
| + | The parameters of the moisture model are set in [[namelist.fire]]. | ||
==Configuration== | ==Configuration== | ||
| + | |||
| + | The moisture properties of the fuels are defined in file [[namelist.fire]]. There is an example in [[https://github.com/jbeezley/wrf-fire/blob/4c0851085eeb25d9143bd5b07e736fe949700497/wrfv2_fire/test/em_fire/moisture '''test/em_fire/moisture''']. | ||
==Standalone diagnostics== | ==Standalone diagnostics== | ||
Revision as of 02:44, 24 December 2012
- Back to the WRF-SFIRE user guide.
Fire spread rate depends strongly on the moisture contents of the fuel. In fact, the spread rate drops to zero when the moisture reaches the so-called extinction value
For this reason, we have coupled the fire spread model with a simple fuel moisture model integrated with WRF and SFIRE. The model takes atmospheric state from WRF and provides fuel moisture to SFIRE.
Fuel moisture model description
The fuel is considered to consist of components - called moisture classes here - such as those with standard 1, 10, and 100 hour lag time. Each fuel category is a mixture of the moisture classes with the proportions given per the fuel category. The temperature and the relative humidity of the air (from the WRF atmosphere model) determine the fuel equilibrium moisture contents. In each class, the moisture contents approaches the equilibrium exponentially in time, with 63% of the difference gone within the given time lag if the equilibrium is constant in time. This is modeled by a standard time-lag differential equation and the class moisture contents generally tracks a time-varying equilibrium with a delay. To model hysteresis effects, there is a higher drying equilibrium and a lower wetting equilibrium; when the fuel moisture is between the two, it does not change. The equilibria are computed from the atmospheric state from WRF. During rain, the equilibrium moisture is replaced by the saturation moisture contents, and the time lag depends on rain intensity. If the rain intensity is under the given rain threshold, no rain wetting (soaking) takes place. For more intense rain, the time lag decreases and approaches the given soaking time lag exponentially, with 63% of the asymptotic value achieved at a given saturation rain intensity.
Calibration of rain wetting
The default rain wetting coefficients were fitted for fine fuels (10 hour moisture class) for the Canadian fire danger rating system. Both pictures show the increase of fuel moisture over 24 hours for a given rain intensity.
The parameters of the moisture model are set in namelist.fire.
Configuration
The moisture properties of the fuels are defined in file namelist.fire. There is an example in [test/em_fire/moisture.
Standalone diagnostics
References
- Adam K. Kochanski, Jonathan D. Beezley, Jan Mandel, and Minjeong Kim, WRF fire simulation coupled with a fuel moisture model and smoke transport by WRF-Chem, 2012 WRF Users Workshop, Poster 51 abstract paper arXiv:1208.1059
- Jan Mandel, J.D. Beezley, A. K. Kochanski, V. Y. Kondratenko, and M. Kim, Assimilation of Perimeter Data and Coupling with Fuel Moisture in a Wildland Fire - Atmosphere DDDAS, ICCS 2012, Procedia Computer Science 9, 2012, 1100-1109